Automated anonymization of documents is one popular research subject and finds extremely important usage in areas like medical data where privacy is taken very seriously. It is in general a difficult task, and even more so for data outside of medical domain due to the lack of specialized tools. In this post, I explored the possibility of using the vector embedding [Mikolov 13] approach to anonymize general forms of documents. I arrived at some interesting results with hints from statistical physics, which I would like share about.

The project: anonymize text documents

Recently, I worked on a consultant project, as a Insight Data Science fellow, partnered with Bonfire, a company based in Ontario, whose main product is a website that helps organizations (universities, hospitals, etc) to setup their procurement processes. Public purchasing often involves some very tedious and tiresome procedures, especially the very early step of preparing a bunch of documents (in jargons: Request For Proposals, or RFPs). Such a pain can be partially reduced if existing documents on similar purchases can be reused by different users as templates. However, for privacy concern, this requires user identifying information in these documents to be removed. So my major goal here is to anonymize the approximately 200,000 documents produced by a couple hundred of users.

It is by no means a task as simple as search-and-replace. In writing the documents, users tend to refer themselves in various ways that cannot be easily categorized. For example, users may mention their building names, street names or even years they were founded, like in the example below.

Name entity recognition seems to be a good start. However, an entity name tagging method is not working very well for documents consisting of unnatural flows of sentences, such as the FAQ style of writing that most of my documents are in. Furthermore, private information is more than just entities.

It boils down to how we define private information. Here is how “privacy” is defined on Wikipedia:

Privacy is the ability of an individual or group to seclude themselves, …

In simple words, what I am after is the information that exclusively belongs to a particular user, but not others. I need to find a way to segment the information within a document according its closeness to a particular user.

Word vectors and context binding

The closeness of information to a given word can be naturally quantified through word vectors in a model called skip-gram [Mikolov 13]. The algorithm trains a vector representation of the vocabulary by binding the context (neighboring words). For any word $w$ and its context word $c$ (or neighbor), this can be achieved by minimizing the negative log-likelihood

$$\begin{equation} l = \sum_{\langle w,c\rangle} \big[ \log(1+ e^{-\boldsymbol{v}_w \cdot \boldsymbol{v}_c}) + \sum_{n\in \mathcal{N}_c}\log(1+e^{ \boldsymbol{v}_w\cdot \boldsymbol{v}_n}) \big ] \end{equation}$$

where $\boldsymbol{v}$ is a mapping from the vocabulary to a vector space, which is exactly what we are trying to learn, and $\langle w,c\rangle$ means a neighboring pair. The second term in the squared brackets is for negative sampling, where $\mathcal{N}_c$ is a set of random negative samples of $c$. It essentially serves as a regularization term.

The context binding here provides a way to separate out the common words. This can be visualized in the cartoon below. Intuitively, when a common word shows up in multiple contexts, the binding will pull it away from any of the contexts, as a compromise to getting close to all of them. As a result, words that are unique or private will be separated from common words and will be binded closer in the vector space through the contexts.

Such a phenomenon sounds very familiar. We can look at an alternative form of Eq. (1). If we ignore the negative sampling term for a moment, and restrict the embedding $\boldsymbol{v}$ to be a unit vector, then

$$\begin{eqnarray} & & \arg \min \sum_{\langle w,c\rangle} \big[ \log(1+ e^{-\boldsymbol{v}_w \cdot \boldsymbol{v}_{c}}) \big] \nonumber\\ & = & \arg \min \sum_{\langle w,c\rangle} \big [ \log( e^{-\boldsymbol{v}_w \cdot \boldsymbol{v}_{c}}) \big ] \nonumber\\ & = & \arg \min (-\sum_{\langle w,c\rangle} \boldsymbol{v}_w \cdot \boldsymbol{v}_{c} ) \end{eqnarray}$$

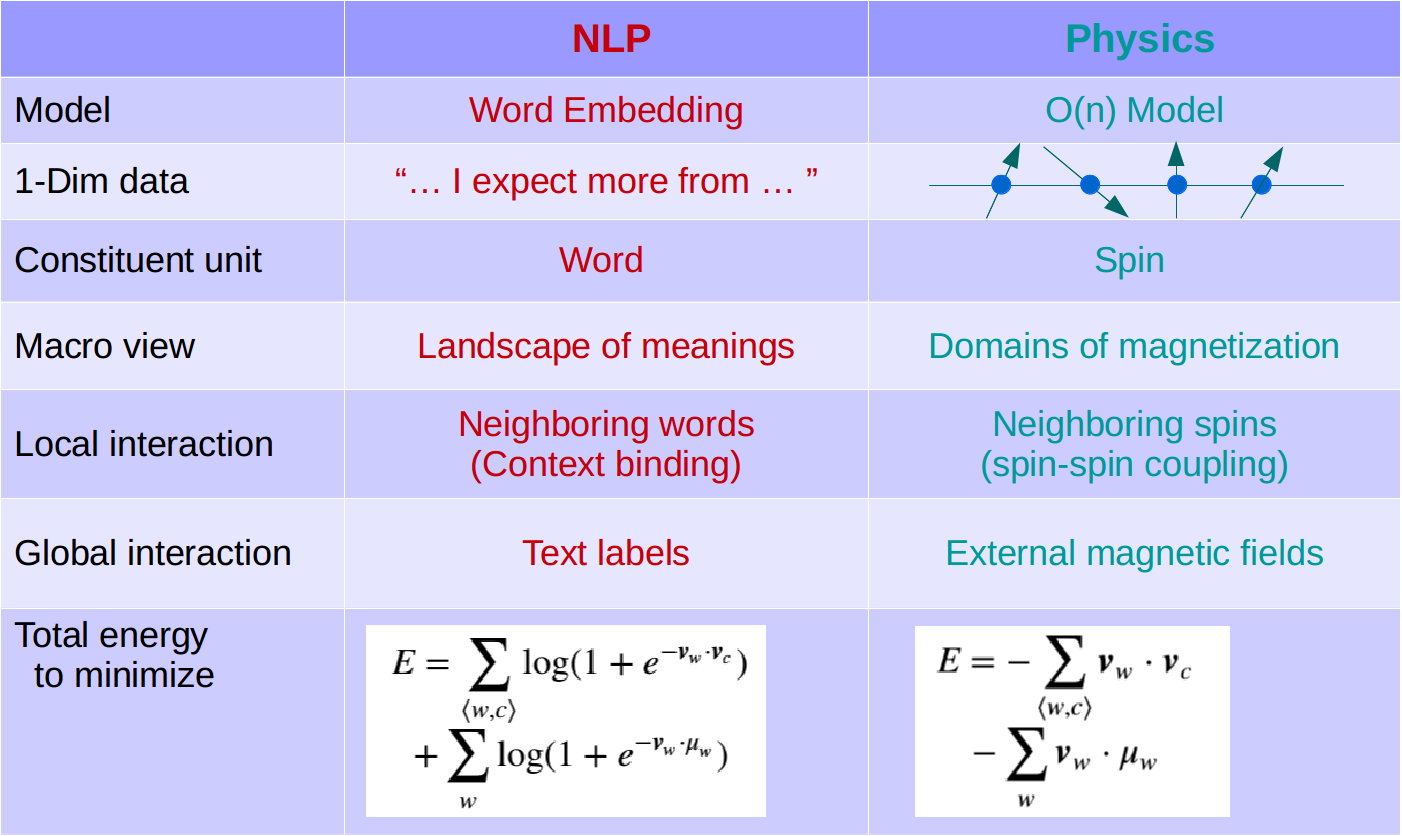
This is nothing but the one-dimensional O(n) model in statistical physics!

The O(n) model or n-vector model is a simplified physics model that explains how macro magnetization is formed as an effect of how grids of the constituent tiny magnets (or spins) line together. Strong magnet field is formed if all the tiny magnets are orientated in the same direction, and otherwise if they are randomly orientated. Every tiny magnet is affecting and affected by its neighbors at the same time. The physics system will settle at around the configuration where the total energy (defined in Eq. (2)) is minimum. Our problem at hand is very similar: we are trying to find a configuration of all the word vectors such that the total “energy” is minimum.

Some additional notes: the special case of O(n) model with $n=1$ is called Ising model, which is one of the most inspiring models that brought us rich insights into the nature of strong coupling systems, such as the fundamental interaction among subatomic particles: quarks and gluons.

Implementation: FastText

My implementation is based on FastText. FastText is an open source library developed by Facebook AI which is based on the skip-gram model that we just discussed, but adding an important ingredient that is highly relevant to our interest here: the sub-word information, based on the character-based n-gram algorithm [Bojanowski&Grave 16]. Its implication here is two-folded. One, it largely reduces out-of-vocabulary scenarios that word2vec might encounter. Second, it can bind words or typos that are morphologically similar, and hence achieve some functionality of “regular expressions”, which is crucial for our anonymization task.

I turned the entire set of documents into one hot word array, after some text preprocessing and cleaning, then fed it to fastText to learn the vector representation. Given a trunk of text, I will be able to calculate the angle separation between any word in the text to a given term, say “Utopia University”, which can then be taken as a score that measures its closeness to such a term. It turned out that this simple method worked very well. With a fairy low false positive rate (3~4%), I was able to identify 75~80% of the sensitive words.

However, there is a caveat in this approach. Since we only use context binding, some word vectors that belong to different users may end up being close because they might largely overlap in some contexts. There is no guarantee that this will not happen.

Some hints can be found in our analog with O(n) model. In Eq. (2), we leave out one important term of the O(n) model. With the presence of an external magnetic field $\boldsymbol{\mu}$, the correct total energy should be

$$\begin{equation} E = - \sum_{\langle w, c\rangle} \boldsymbol{v}_w \cdot \boldsymbol{v}_c - \sum_{w} \boldsymbol{v}_w \cdot \boldsymbol{\mu} \end{equation}$$

The physical implication here is straightforward: every tiny magnet goes under the shadow of its neighbors and the external field. Our word embedding problem is similar. The words in a labeled document are essentially under the shadow of a “external field” (the label). So inspired by the O(n) model, we should add the counterpart to the negative log-likelihood, which is missing in the skip-gram model. That was essentially what I did, adding a term

$$\begin{equation} \sum_w \log(1+ e^{-\boldsymbol{v}_w \cdot \boldsymbol{\mu} }), \end{equation}$$

which I called a polarization term, to the skip-gram model. The comparison is summarized in the following table.

Improvement: PolarizedText

To integrate the polarization term (Eq. (4)), I had to modify the source code of fastText and made a new repository called PolarizedText. PolarizedText puts each document label into its unique dimension and applies an “external field” (the label) to shadow the text. This avoids the label confusion that might happen during the context binding. Furthermore, the separations of the unique words are maximized since they are orthogonal.

Result

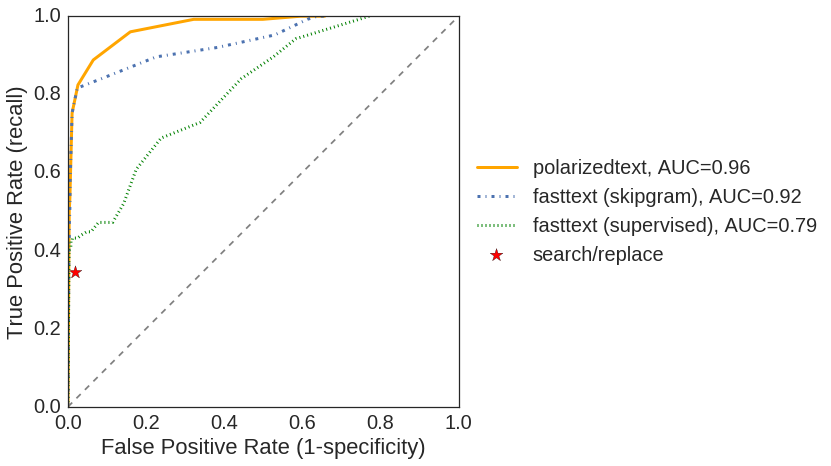
To validate the algorithm, I hand labeled about 300 documents for the words that subject to removal. The ROC curves of various methods are compared below. The curves are obtained by varying the removal threshold (word vector cosine similarity). The difference between the “fasttext(supervised)” and “fasttext(skipgram)” approaches is that the latter enforces context binding while the first doesn’t. In a sense, “polarzedtext” synthesizes the two approaches, and the plot indicates that it is beneficial to do so. The anonymizer based on PolarizedText outperforms those based on FastText, showing that the polarization step helps the word embedding, due to a reason that is hinted in physics.

slides

---

[Mikolov13] Tomáš Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013b. Distributed representations of words and phrases and their compositionality. In Adv. NIPS

[Bojanowski&Grave 16] P. Bojanowski, E. Grave, A. Joulin, T. Mikolov, Enriching Word Vectors with Subword Information, arXiv:1607.04606